Persistent Super Achiever Test 2023
Super Achiever Test Persistent for 2023
Persistent has announced its on-campus hiring for 2023 engineering graduates. This year hiring pattern of Persistent is totally different from what they have been following in the past. This year Persistent is offering 3 different roles and packages to the graduates of 2023. Based on the performance in the hiring exam students can get a package ranging from 5LPA to 9LPA

What is Persistent Super Achiever Test ?
Persistent has changed its hiring pattern for 2023 graduates. Super Achiever Test is a new section being introduced by Persistent. This is the final round of recruitment exam. Only those candidates who have cleared the first two rounds of the hiring i.e; Objective+Subjective Round and Advanced Coding Round are eligible for this round. Clearing this round will increase your package from 7.8 LPA to 9.3 LPA.
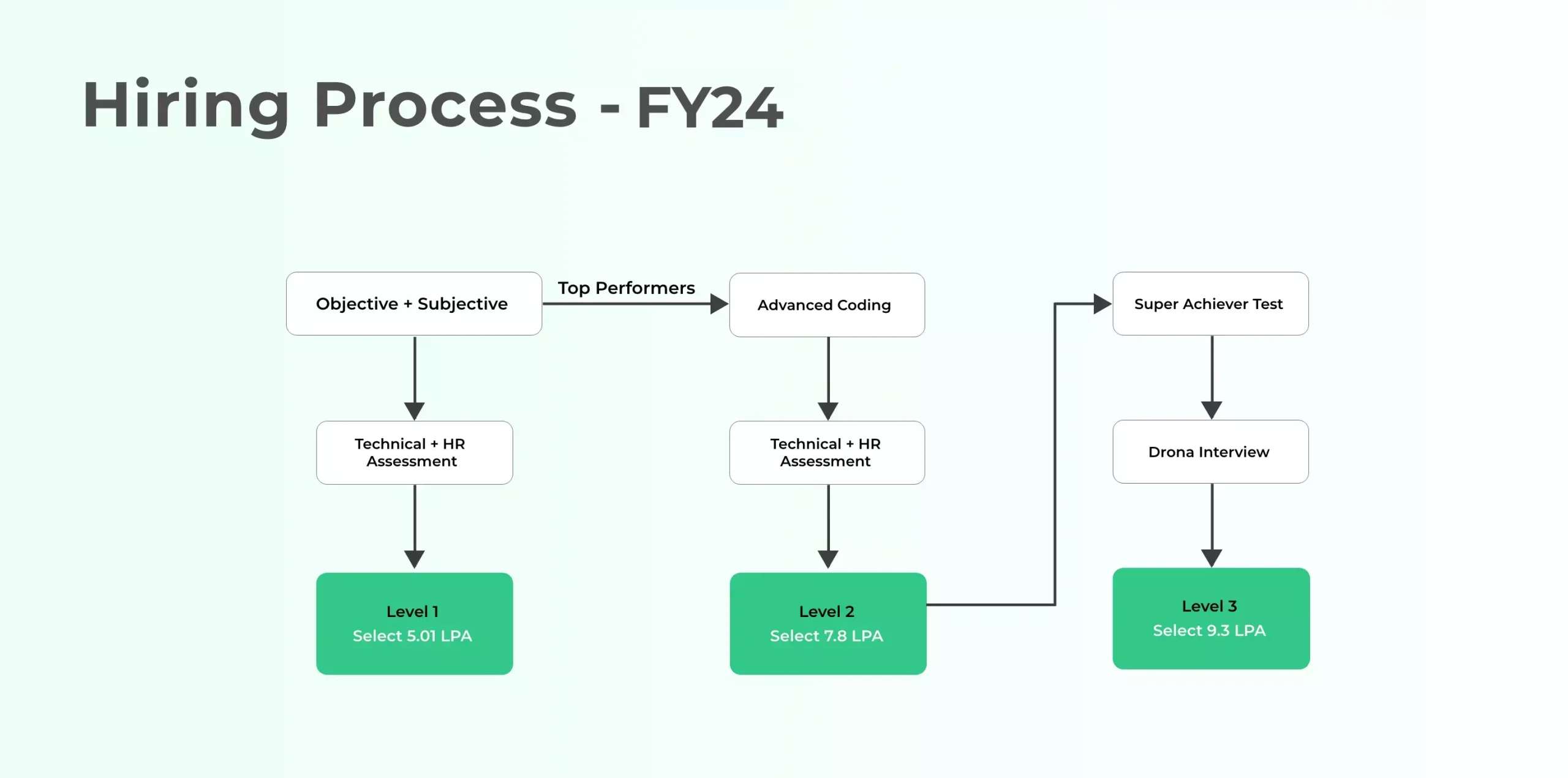
What rounds are asked in Super Achiever Test ?
This section consists of 2 rounds.
- Super Achiever Test
- Drona Interview
Super Achiever Test – Persistent has not announced yet what exactly will be asked in this particular test, but based on our research we can tell you either this will be a coding round with advance coding topics like dynamic programming, multithreading, exceptional handling, greedy algorithms, etc. or it will be a after placement test, based on the training that you’ve under gone and then there will be an internal test, wherein you get a chance of increasing you offer and get a better role.
Drona Interview – After clearing the super achiever test round, you will be facing the final interview round i.e; Drona Interview, this is just another interview which will be based on the above round problem statement. Clearing this interview round will give you a package of 9.3 LPA.
Question 1: Longest Increasing Subsequence (LIC)
Given an integer array ‘A’, find the length of its Longest Increasing Subsequence(LIS). LIS is a sub-array of the given integer array where the elements are sorted in a monotonic/ strict increasing order.
You need to fill in a function that takes two inputs – integer ‘n’ and an integer array ‘A’ containing ‘n integers and returns the length of its LIS.
Input Specification:
input1: integer input ‘n'(1 <= input1 <= 1000)
input2: integer array ‘A’ input, containing ‘n’ integers.
Output Specification:
Return the length of its LIS.
Example1:
Input1: 3
Input2: (1,3,2)
Output: 2
Explanation:
(1.2) and (1.3) are the longest increasing subsequences of (1,3,2). The length of both LIS is 2.
Example 2:
input1:5
input2: (41, 18467,6334 26500, 19169)
Output: 3
Explanation:
(41,6334,26500), (41,18467 26500), etc are the longest increasing subsequences of (41, 18487,6334 ,26500,19169). In all of the cases, the length of LIS is 3.
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
int arr[n];
for (int i = 0; i < n; i++)
cin >> arr[i];
int dp[n];
int ans = 0;
for (int i = 0; i < n; i++)
{
dp[i] = 1;
for (int j = 0; j < i; j++)
{
if (arr[j] < arr[i])
{
dp[i] = max(dp[j] + 1, dp[i]);
}
}
ans = max(ans, dp[i]);
}
cout << ans << endl;
return 0;
}
import java.util.*;
public class Main{
public static int longestIncreasingSubsequence(int arr[], int n)
{
int dp[]=new int[n];
int res=0;
for(int i=0;i<n;i++)
{
dp[i]=1;
for(int j=0;j<i;j++)
{
if(arr[j]<arr[i])
dp[i]=Math.max(dp[i],dp[j]+1);
}
res=Math.max(res,dp[i]);
}
return res;
}
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] arr=new int[n];
for(int i=0;i<n;i++)
arr[i]=sc.nextInt();
System.out.println(longestIncreasingSubsequence(arr,n));
}
}
def ceilindex(t,l,r,key):
while(r-l>1):
m=l+(r-l)//2
if(key<=t[m]):
r=m
else:
l=m
return r
def lcs(a,n):
seq=[0 for i in range(n)]
seq[0]=ar[0]
l=1
for i in range(1,n):
if(seq[0]>a[i]):
seq[0]=a[i]
elif(a[i]>seq[l-1]):
seq[l]=a[i]
l+=1
else:
seq[ceilindex(seq,-1,l-1,a[i])]=a[i]
return l
n=int(input())
ar=list(map(int,input().split()))
print(lcs(ar,n))
Question 2: Arithmetic Progression(AP)
Given the second and the third terms of an AP (-106 <= a2, a3 <= 106), find the n’th (1 <= n <= 1000) term of the sequence.
Input Specification:
input1: Second element of series (Integer).
input2: Third element of series (Integer).
input3: Total number of elements in the series (Integer).
Output Specification:
Return the nth element of the series.
Example 1:
input1:1
input2: 2
input3: 4
Output: 3
Example 2:
input1: 5
Input: 8
Input3: 4
Output: 11
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
ll sec,third,n;
cin>>sec>>third>>n;
ll d = third - sec;
ll first = sec-d;
ll nth = first + (n-1)*d;
cout<<nth<<endl;
return 0;
}
import java.util.*;
public class Main{
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int second=sc.nextInt();
int third=sc.nextInt();
int n=sc.nextInt();
int d=third-second;
int first=second-d;
int nth=first+(n-1)*d;
System.out.println(nth);
}
}
secondTer=int(input()) ThirdTer=int(input()) n=int(input()) d=ThirdTer-secondTer firstTer=secondTer-d print(firstTer + (n-1)*d)
Question 3: Mr. Myers and the Exam
A mathematics question paper has a certain number of questions and each question is assigned some random maximum marks. Mr. Myers wants to edit the marks assigned to the questions such that.
- All questions in the paper should have distinct maximum marks
- The total marks of all the questions should be as low as possible.
Mr. Myers wants to achieve this by making minimal changes in the original format, assigning the question at least as much marks as it originally had. Find the minimum total marks that he can set the paper for
Input Specification:
input1: The number of questions in the paper
input2: The array representing the original marks assigned to every question
Output Specification:
The minimum total marks Mr. Myers can set the paper for
Example 1:
input1: 5
input2: {1,2,3,4,5)
Output: 15
Explanation:
As all the questions already have distinct marks he can set the paper as it is with minimum marks as 1+2+3+4+5 = 15
Example 2:
input1: 5
input2: {1,4,5,4,5)
Output: 23
Explanation:
Here the question 1 would have at least 1 mark, question 2 would have at least 4 marks question 3 would have at least 5 marks, so the new set of marks will have to be {1,4,5,6,7}, such that all the conditions are satisfied.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
int n;
cin >> n;
ll arr[n];
for (int i = 0; i < n; i++)
cin >> arr[i];
sort(arr, arr + n);
ll prev = arr[0];
ll ans = arr[0];
for (int i = 1; i < n; i++)
{
ll cur = arr[i];
if (prev > cur)
{
cur = prev + 1;
}
else if (cur == prev)
{
cur++;
}
ans += cur;
prev = cur;
}
cout << ans << endl;
return 0;
}
import java.util.*;
public class Main{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n=sc.nextInt();
int arr[]=new int[n];
for(int i=0;i<n;i++)
arr[i]=sc.nextInt();
Arrays.sort(arr);
int prev=arr[0];
int res=arr[0];
for(int i=1;i<n;i++)
{
int curr=arr[i];
if(prev>curr)
curr=prev+1;
else if(curr==prev)
curr++;
res+=curr;
prev=curr;
}
System.out.println(res);
}
}
n=int(input())
ar=list(map(int,input().split()))
ar.sort()
ans=ar[0]
prev=ar[0]
for i in range(1,n):
if(ar[i]>prev):
ans+=ar[i]
elif(prev >= ar[i]):
ar[i]=prev+1
ans+=ar[i]
prev=ar[i]
print(ans)
Question 4: Street Lights
One of the streets in your city has a total of L street lots. Each light covers the street from Xi to Y
Input Specification
Input1: L,i distance. Find the length of the street covered with light. denoting the number of street lights
Input2: An array of L * 2 elements. For each row i, (Xi, Yi) denote that the street light i covers the distance from Xi to Yi.
Output Specification:
Your function should return the length of the street covered with light.
Example 1:
Input1: 1
Input2: {(5, 10)}
Output: 5
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
pair<int, int> arr[n];
for (int i = 0; i < n; i++)
{
cin >> arr[i].first >> arr[i].second;
}
// sorting by x values
sort(arr, arr + n);
int x = INT_MIN;
int y = INT_MIN;
long long ans = 0;
for (int i =0;i<n;i++)
{
int curX = arr[i].first;
int curY = arr[i].second;
if(y<=curX)
{
ans+=(curY-curX);
x = curX;
y = curY;
}
else if(x<=curX && curX<=y && curY>=y)
{
x = y;
y = curY;
ans+=(y-x);
x = curX;
}
else // previous point completly overlaps new point
{
continue;
}
}
cout<<ans<<endl;
}
import java.util.*;
public class Main
{
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int arr[][]=new int[n][2];
for(int i=0;i<n;i++)
{
for(int j=0;j<2;j++)
arr[i][j]=sc.nextInt();
}
int sum=0,diff=0;
for(int i =0;i<arr.length;i++){
sum = sum +(arr[i][1]-arr[i][0]);
if(i<arr.length-1){
if(arr[i][1] > arr[i+1][0] || (arr[i][1] - arr[i+1][0]) == -1){
diff = diff +(arr[i][1] - arr[i+1][0]);
}
}
}
System.out.println(sum-diff);
}
}
l=int(input())
ar=[]
for i in range(l):
a,b=map(int,input().split())
ar.append((a,b))
ar.sort(key=lambda x: x[0])
ans=ar[0][1]-ar[0][0]
y=ar[0][1]
for i in range(1,l):
if(y>=ar[i][0]):
ans=max(ans, ans+(ar[i][1]-ar[i][0]) - (y - ar[i][0]) )
else:
ans+=(ar[i][1]-ar[i][0])
y=max(ar[i][1],y)
print(ans)
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates
