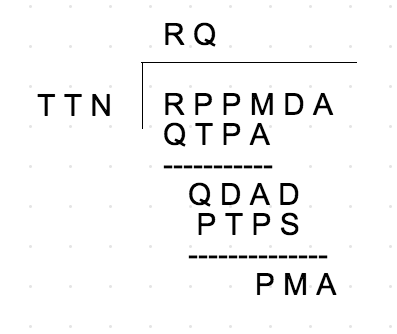
Cryptarithmetic Division Problem 4

Breaking down the problem -
  T T N
  x   R
------- - 1
Q T P A

  T T N
  x   Q
------- - 2
P T P S

  R P P M
- Q T P A
--------- - 3
    Q D A

Now lets take equation number 3

From 10's digit we see that P - P = D,
Thus it is clear that value of D = 0
and possible values of P can be = {1,2,3,4,5,6,7,8,9}

Now, Learn this Cryparithmetic Subtraction Rule -
If, X - A = A,
Then X = {2, 4, 6, 8}
A = {1, 2, 3, 4}

Thus, in our case M - A = A
So, they will have values,
M = {2, 4, 6, 8}
A = {1, 2, 3, 4}
Now, lets do hit and trial method,

D = 0, M = 2, A =1
So, possible values for P = {1,2,3,5,6,7,9}
R is not 1 as R > Q and if R is 1 then there is no value of Q.
Let us assume P = 5

  R 5 5 2
- Q T 5 1
---------
    Q 0 1

Since, R - Q is 0. Thus, R and Q must be consecutive.
i.e. R = Q + 1
Possible values for R and Q can be = 
{(7,6)}

As, (1,2) not possible as (M,A) are there.
As, (2,3) not possible as M is 2

Next consecutive value are (5,6)
P is already 5
So (R,Q) cant be (6,5)

If (P,Q) = (7,6)
  7 5 5 8
- 6 T 5 4
---------
    6 0 4

Now, for 5 - T = 6
T = 9, thus possible.

Putting these in Eq - 1

  9 9 N
x     7
-------
6 9 5 1

Since, N x 7 = _1. Thus, N = 3(as 21)

Putting all these values

       _________
9 9 3 |7 5 5 2 0 1
       6 9 5 1
       -------
         6 0 1 0
         5 9 5 S
        --------
             5 2 1

Clearly S = 8
Thus, we have found all values.