PrepApti - Quants Menu
- Home
- Allegations and Mixtures
- AP GP HP
- Arithmetic Progressions
- Averages
- Boats and Streams
- Geometric Progressions
- Harmonic Progressions
- Clocks
- Calendar
- Clocks and Calendars
- Compound Interest
- Simple Interest
- Simple Interest and Compound Interest
- Linear Equations
- Quadratic Equations
- Co-ordinate geometry
- Perimeter Area Volume
- Divisibility
- HCF and LCM
- HCF
- LCM
- Number System
- Percentages
- Permutations Combinations
- Combinations
- Piipes and Cisterns
- Probability
- Work and Time
- Succesive Discounts
- Heights and Distance
- Decimals and Fractions
- Logarithm
- Venn Diagrams
- Geometry
- Set Theory
- Problem on Ages
- Inverse
- Surds and Indices
- Profit and Loss
- Speed, Time and Distance
- Algebra
- Ratio & Proportion
- Number, Decimals and Fractions
How to Solve Elementary Statistics Quickly
How to solve Elementary Statistics Quickly
Elementary Statistics is most frequently asked topic in the placement papers. The common mistake done by students is that they take this topic lightly and ignore this section. This is one of the scoring section.Go through this page to know about How to Solve Elementary Statistics Quickly.
Points to Remember while Solving Statistics Problem
There are few things to keep in mind while solving statistics problem:
Stay focused and don’t be panic:
When students get the question usually they need to be more focused and calm at the same time.This will help them to make a right approach to solve the question.
Analyze the Problem:
Instead of attempting the question immediately give some time on the question.Analyze the question properly and then attempt the question.This will eliminate the chances of making mistakes.
Go for the right strategy:
If you are going for right strategy your chances for making mistakes will be eliminated and time taken to solve the problem will be minimized so it will allow you to solve the problem within limited time.
How to Solve Elementary Statistics Quickly
Directions for question 1 and 2 – Visualize the graph and solve the following questions:
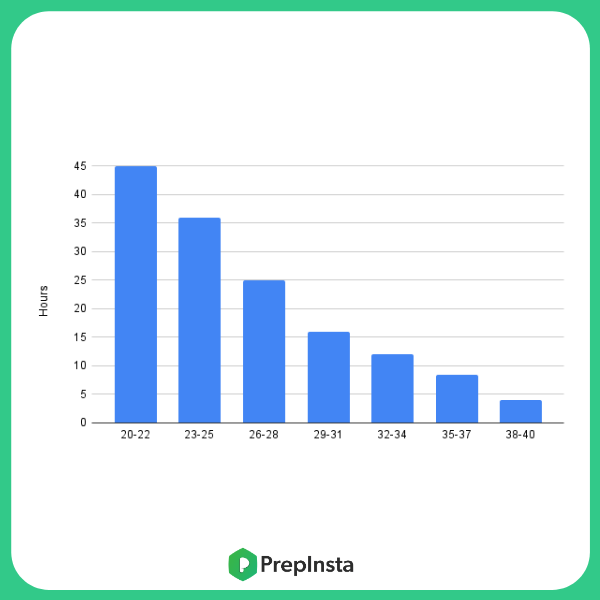
The chart indicates the amount of time spent in hours by people of age group between 20-40 years on mobile phones each week.
Example 1: Find the mean of the hours spent on the phone by all the age groups.
Solution: From the given graph we get the following set of data 45,36,25,16,12,8.5,4
Mean= \frac {\text{sum of all the elements}}{\text{number of elements}}
= \frac{45+36+25+16+12+8.5+4}{7}
= \frac{146.5}{7}
=20.92
Hence,the mean of the data will be 20.92
Example 2: Similarly if we have to find the median of the given set of data.
Solution: Median is the middle value of a set of data.so here median is 16.
Example 3: Evaluate the following for given set of numbers:
3 \times mean+2\times mode – 6 \times medianSet={1, 2, 2, 3, 3, 3, 4, 4, 4, 4}
Solution: As we know that mode of a given set of numbers is the observation or number which occurs most frequently.
Clearly numbers are arranged in ascending order
So, mode = 4
median= \frac{(3+3)}{2}=3
mean= \frac{30}{10}=3
So,
3 \times mean+2\times mode – 6 \times median
= 3 \times 3 + 2 \times 4 – 6 \times 3
= 9 + 8 – 18
= 17 – 18 = -1
Example 4: Runs scored by Virat Kohli in some 3 test Matches against Australia are as follows 101, 126, 32, 38, 52, and 40. Find median of the given scores.
Solution: Arranging in ascending order 32,38,40,52,101,126
Median = \frac{1}{2}[\frac{n}{2}+\frac{n+2}{2}]th term..for n = even
⇒Median= \frac{40+52}{2}=\frac{92}{2}=46
Example 5: The numbers of rupee notes of different denominations are given as below.
| Denomination | 10 | 20 | 05 |
|---|---|---|---|
| Number of Notes | 15 | 20 | 8 |
Find mode of above data
Solution: Mode is the most number of repeated data in a set.Here,Clearly ‘20’ is repeated twice so, mode = 20
Example 6:Find the variance and the standard deviation from the given data.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|---|
| Frequency | 27 | 10 | 7 | 5 | 4 | 2 |
Solution:
N=\sum f=55 Mean=\frac{\sum fx_{i}}{N}= \frac{925}{55} =16.818
Variance= \frac{1}{N-1}[\sum fx_{i}^{2}-\frac{1}{N}(\sum fx_{i}^{2})]
= \frac{1}{55-1}[27575-\frac{1}{55}({925}^{2})]
= \frac{1}{54}[27575-15556.8182]
=222.559
Standard deviation= \sqrt{variance}
= \sqrt{222.559}
= 14.91
| Class Interval | Frequency | Mid Value x_{i} | fx_{i} | fx_{i}^{2} |
|---|---|---|---|---|
| 0-10 | 27 | 5 | 135 | 675 |
| 10-20 | 10 | 15 | 150 | 2250 |
| 20-30 | 7 | 25 | 175 | 4375 |
| 30-40 | 5 | 35 | 175 | 6125 |
| 40-50 | 4 | 45 | 180 | 8100 |
| 50-60 | 2 | 55 | 110 | 6050 |
| \sum f=55 | \sum fx_{i}=925 | \sum fx_{i}^{2}=27575 |

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates

Login/Signup to comment