Cryptarithmetic Division Problem 3
First we will convert this question into multiple, Cryparithmetic Multiplication Problems –
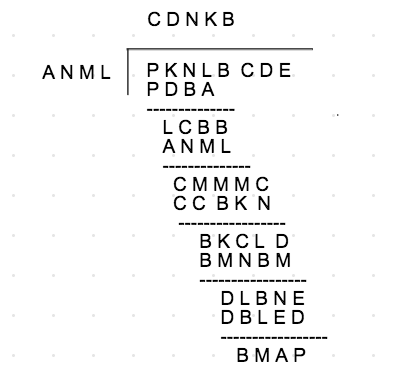
Before that in 4th row you see ANML and the divisor is also ANML, so value of D = 1 clearly.
PT
As,
A N M L
x D
--------
A N M L
thus, D = 1.
C 1 N K B
_______________
A N M L |P K N L B C 1 E
P 1 B A
--------------
L C B B
A N M L
--------------
C M M M C
C C B K N
-----------------
B K C L 1
B M N B M
-----------------
1 L B N E
1 B L E 1
-----------------
B M A P
Check Unit digit method here.
Now, Find the multiplication with most substituted values,
it is -
A N M L
x B
--------
1 B L E 1
Now, using Unit digit's method possible ways of getting 1 are
(check the link above for Unit digit method to find all rules)
3 x 7 = _1 (21 only last digit considered)
7 x 3 = _1 (21 only last digit considered)
Thus, values are
either L = 3, B = 7 and L = 7, B = 3
using case 1 first,
A N M 3
x 7
---------
1 7 3 E 1
Now, if you consider A x 7, this results in 17.
There is only one possibility, for A x 7 + carry = 17
when A = 2 and carry = 3( A = 1 not possible as
7 + 6(max carry ie 7 x 9 =63) results only in 13 which is <17.
So now eqn is
2 N M 3
x 7
---------
1 7 3 E 1
Now, we know what carry from 7 x N was 3, this is only possible when
7 x N = _3 when N = 4( 28 + some carry >=2)
or 5( 35 + some carry less equal to 4)
Taking N = 4,
2 4 M 3
x 7
---------
1 7 3 E 1
Now, at unit's digit 3 value and 3 as carry.
It is possible for 7 x 4 + 5(carry) = 33
Now to get 5 carry from last step
you have to multiply 7 with either 7 or 8
Now, take M = 8
2 4 8 3
x 7
---------
1 7 3 E 1
Now carry from unit's 7 x 3 will be 2
and 7 x 8 + 2 carry = give value of E = 8. and M also 8. So, not possible.
Sim. M = 7 is not possible(try yourself)
Now try L = 7 and B = 3
A N M 7
x 3
---------
1 3 7 E 1
Now A = 4 to get 13 with 1 carry from prev. multiplication,
1
4 N M 7
x 3
---------
1 3 7 E 1
Now, to give 1 carry and 7 at unit's place
value of N = 5 with 2 carry from previous operation
1 2
4 5 M 7
x 3
---------
1 3 7 E 1
Now, 3 x M can give 2 carry for M={6, 8, 9}
Let's do hit and trial. Take M = 6.
1 2 2
4 5 6 7
x 3
---------
1 3 7 E 1
Now, 3 x 7 gives 2 carry to next mult.
and
3 x 6 + 2 as carry = 20 so E = 0.
1 2 2
4 5 6 7
x 3
---------
1 3 7 0 1
E = 0, D = 1, A = 4, N = 5, M = 6 its easy to find other values too.
PT




Login/Signup to comment