HCM & LCM Quiz – 1
One Subscription, For Everything
The new cool way of learning and upskilling -
One Subscription access everything
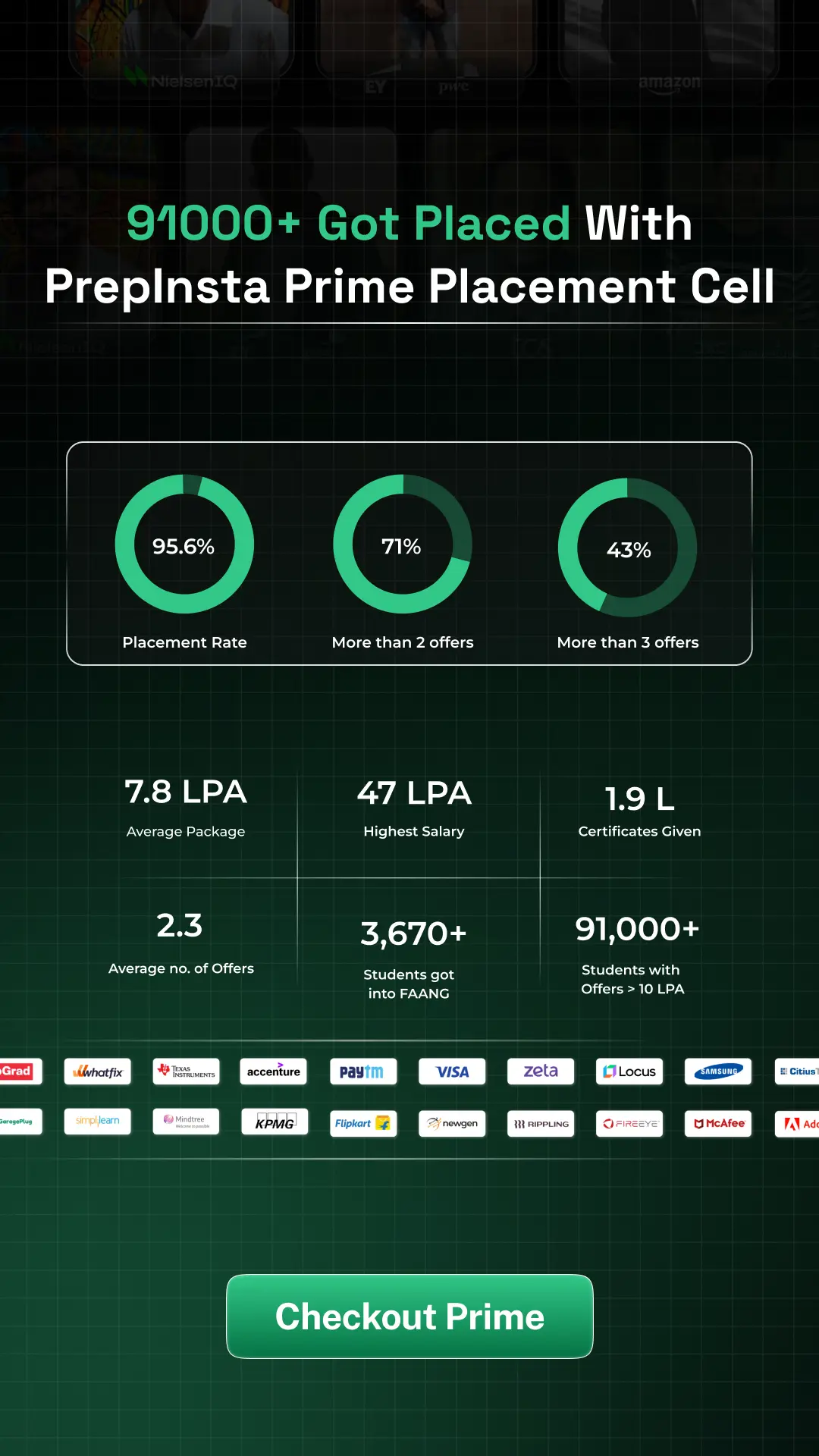
Get Access to PrepInsta Prime
from FAANG/IITs/TOP MNC's

PrepInstaPrime
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others.

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates