Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
PREPINSTA PRIME
Heights and Distance Questions and Answers
Heights and Distance Questions
In this page we will recap through some basic information related to Heights and Distance and then we will be solving Heights and Distance Questions and Answers. Heights and Distance is an important topic for examination point of view. The topic comprises questions where height of a building, angle of elevation, and depression are given for another building, which is close by.
Terms
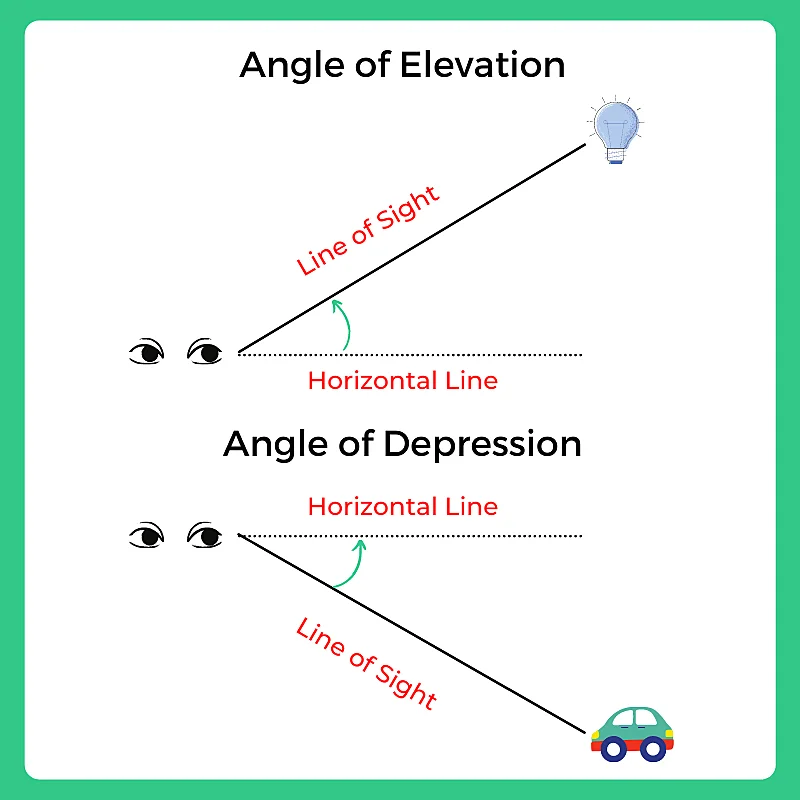
The angle of Elevation
It can be better understood by considering a situation where a person is standing on the ground and looking at an object which is present at some height, for instance, at the top of a building. In this case, the line that joins the eye of the man with the top of the building is known as the line of sight. The angle which is between the line of sight with the horizontal line is known as the angle of elevation.
The angle of Depression
In another situation where a person is standing at some height with respect to an object he is seeing. Here, also the line joining the eye of the man with the building’s bottom is called the line of sight. The angle made by the line of sight with the horizontal line is known as the angle of depression.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Also Check Out
Circular Permutation Questions and Answers

Please login to report
Also Check Out
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Geometry – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Perimeter Area and Volume – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Coordinate Geometry – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Venn Diagrams – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Set Theory – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Geometry – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Perimeter Area and Volume – Questions
Formulas |
How to Solve Quickly
Tricks & Shortcuts - Coordinate Geometry – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Venn Diagrams – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Set Theory – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts


30+ Companies are Hiring
Get Hiring Updates right in your inbox from PrepInsta

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates

