How To Solve Number Series Question Quickly

August 10, 2023

How to Solve Number Systems Problems Quickly in Logical

Here , In this Page How to Solve Number Series Questions Quickly is given.

Number system is the standard of representing numbers . The same sequence of numbers or symbols may represent different value of numbers in different numeral systems.

In this Page different types of Questions is also given and shown how to solve the questions.

How to Solve Number Series Questions Quickly

Solving Number Series Questions Effectively Tips and Tricks

  • There are following types of number Series patterns –
    1. Numeric Number Series (This page)
    2. Alphabet Series (Visit Alphabet Series Page)
    3. Alpha Numeric Series(Not asked in Placements, only in CAT exam)
  • There are the following most popular number series, We will discuss all these in details here we are just introducing them to you, so don’t worry if you don’t see the pattern just yet, after this post you will be able solve any Number Series Question in the world .

Types of Number Series Problems –

  • Add up Series (+) :  Just adding a constant number everytime. For example:  (13, 18, 23, 28 ….).
  • Add up Series (- ):  , Just subtracting a constant number every time. For example : (28, 23, 18, 13 ……).
  • Step up Series (+/-) :  Adding/Subtracting a variable number, in this case we are adding 2n for n = 0, 1, 2, 3 …… For example : 0, 2, 6, 12, 20…. or 20, 12, 6, 2, 0, 0 …..
  • Square up (+/-) –  Given series is in the square of n where  n= 1,2,3,4,5,6… i.e. 1,4,9,16,25,36…
  • Square add up Series(+/-) : Adding n2 every time and incrementing value of n starting from 1 i.e. 1,5, 14, 30, 55, ……  and Subtracting n2 every time and decrementing value of n i.e. 34, 33, 29, 20,
  • Cube Up Series : Given series is in the cube of n where n = 1,2,3,4,5,6… i.e. 1,8,27,64,125,216….
  • Cube add up Series : Adding n3 every time with incrementing of n by 1 i.e. 1,9,36…
  • Prime up(+/-) : Sequence consist of Prime numbers i.e. 2,3,5,7,11…
  • Prime Square up(+/-) : Sequence consist of squares of prime numbers i.e. 4,9,25,49,121..
  • Arithmetic Series: Sequence consist of Arithmetic Progression i.e. 3,6,9,…
  • Geometric Series : Sequence consist of Geometric Progression i.e. 2,6,18,54,…

Now lets try to learn each of these in detail, do let us know in comments section if you’re not able to understand any problem concept, we will help you out with alter logic.

  • Probability of asking – Medium
  • Difficulty – Low
  • Reason –  Infosys, IBM etc
  • After our concept you will always be able to solve this problem and will always look easy, but had you not been reading this 30% students are not able figure out correct series of such problems
  • Probability of asking – Low
  • Difficulty – Hard
  • Reason – Infosys(very rarely) etc
  • After our concept you will always be able to solve this problem and will always look easy, but had you not been reading this 90% students are not able figure out correct series of such problems
  • Probability of asking – Medium
  • Difficulty – Hard
  • Reason – Infosys, IBM.  etc
  • After our concept you will always be able to solve this problem and will always look easy, but had you not been reading this 70% students are not able figure out correct series of such problems

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

How to Solve Number Series Questions Quickly

  •  Number series:
    • A series of different numbers following some logical pattern of various mathematical concepts. One has to analyze the concept used and accordingly find out the missing number of the series.

Generally, there are 5 different types of series, which are explained below with examples:

Type 1.How to Solve Number Series Questions Quickly  – Perfect Square questions

Question 1. Find the missing numbers from the series?

225, 256, 289, —, 361—, 441

Options:

A.  324, 400

B.  325, 450

C.  320, 392

D.  None of the above

 

Solution:    (15)2= 15 x 15= 225

(16)2= 16 x 16= 256

(17)2= 17 x 17= 289

(18)2= 18 x 18= 324

(19)2= 19 x 19= 361

(20)2= 20 x 20= 400

(21)2= 21 x 21= 441

Correct option: A

Question 2. Find the missing number from the series?

4, 16, 36, –, 100, —, 196

Options:

A.  49, 121

B.  64, 144

C.  81, 169

D.  None of the above

Solution:    Here the series contains a perfect square of ever alternate even number like

2 x 2 = 4

4 x 4 = 16

6 x 6 = 36

8 x 8 = 64

10 x 10 = 100

12 x 12 = 144

Correct option: B

Question 3. Find the wrong number in the series?

50, 75, 111, 160, 225

Options:

A.  181

B.  224

C.  225

D.  None of the above.

 

Solution:    Here the first number is 50 which is not a perfect square, the next number is 75, which again is not a perfect square. Hence this is evident that the series is not a perfect square series, but the difference between the two perpetual numbers of the series is 25 (75-50), 36 (111-75), 49 (160-111) and all these numbers are perfect squares, Hence the next number shall be 160+64= 224 But here its 225, Hence Option C is the correct One.

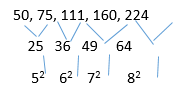
Correct option: C

 

Type 2. How to Solve Number Series Questions Quickly : Perfect cube series

  • Such series consists of numbers that perfect cubes. Some of its examples are mentioned below:

Question 1. Fill in the blank with a number that will follow the below-mentioned series?

343, 729, —-, 2197, 3375

Options:

A.  1331

B.  1000

C.  4096

D.  None of the above

Solution:    This series consists of perfect cubes of perpetual odd numbers beginning from 7. Like 7, 9, 11, 13, 15 and so on.

343 (7 x 7 x 7)

729 (9 x 9 x 9)

1331 (11 x 11 x 11)

2197 (13 x 13 x 13)

3375 (15 x 15 x 15)

Correct option: A

Question 2. There is one wrong number which is not following the pattern of the series. Find out that number from the options given below?

2197, 5832, 12168, 21952, 35937

Options:

A.  12168

B.  2197

C.  21952

D.  35973

Solution:     133= 2197

183= 5832

233= 12167

283= 21952

333= 35952

In this series 5 is added to each cube digit to get the next cube number. Like (13+5)= 18; (18+5)= 23….

Correct option: A

Question 3. Find the missing numbers from the series?

9261, 32768,——– , 157464, 274625,———

Options:

A.  79507, 438976

B.  81454, 398676

C.  68921, 45887 6

D.  None of the above.

Solution:    213 = 9261

323 = 32768

433 = 79507

543 = 157464

653 = 274625

763 = 438976

Here 11 is added to each cube digit to get the next cube number like 21+11= 32

31+11= 43 and so on.

Correct option: A

Type 3. How to Solve Number Series Questions Quickly : Ration Series

  • This series contains numbers arranged in a particular order, and there is a set pattern of variance between each digit of the series. Now we have to analyze that pattern and accordingly calculate the next missing number of the series.
  • This is explained with a couple of examples mentioned below:

Question 1. Find the missing numbers from the series?

12, 24, —, 96, —, 384

Options:

A.  48, 192

B.  36, 108

C.  72, 288

D.  None of the above.

Solution:     In this series, it is evident that 2 is multiplied to each consecutive number to get the next number. Which is mentioned below:

12 x 2 = 24

24 x 2 = 48

48 x 2 = 96

96 x 2 = 192

192 x 2 = 384

Therefore option A is the correct one.

Correct option: A

Question 2.  Which one is/are the wrong number which is not following the series trend?

12, 24, 48, 816, 16214, 32424

Options:

A.  16214

B.  12, 24

C.  48, 816

D.  32424

Solution     If we separate unit digit of the number:

(1+1= 2; 2+2= 4)= 24

(2+2= 4; 4+4= 8)= 48

(4+4= 8; 8+8= 16)= 816

(81+81= 162; 6+6= 12)= 16212

(162+162= 324; 12+12= 24)= 32424

Hence option A is the correct one.

Correct option: A

Question 3.  Find the missing numbers from the series below?

3, 21, 147, —, 7203, —-

Options:

A.  2209

B.  1029

C.  6172

D.  None of the above

Solution:    This series consists of a sequence where each number is multiplied by 7:

3

3 x 7 = 21

21 x 7 = 147

147 x 7= 1029

1029 x 7 = 7203

7203 x 7 = 50421

Correct option: B

Type 4. How to Solve Number Series Questions Quickly  : Geometric series

  • Geometric series is a formula based series wherein the missing number is calculated by either adding, multiplying, subtracting or dividing the consecutive term with a constant number.

Its formula is mentioned below:

G S= {a, ar, ar2, ar3,….}

Where the a= first term of the series

R= factor or difference between the term, also known as the common ratio.

Question 1. Find the missing numbers from the below-mentioned series?

1, 3, 9, 27 , –, 243, —

Options:

A.  81, 729

B.  27, 729

C.  81, 486

D.  None of the above

Solution:    Here a = 1 (first term of the series)

R = 3 ( common number that is multiplied with the consecutive number of the series)

Hence we get:

1

1 x 3

1 x 32 = 9

1 x 33 = 27

1 x 34 = 81

1 x 35 = 243

1 x 36 = 729

Correct option: A

Question 2. Find the wrong number which does not follow the series pattern?

5, 7, 15, 35, 77 , 161

Options:

A.  15

B.  5

C.  7

D. 35

E.  112

F.  455

Solution:    5 x 0 + 7= 7

7 x 1 + 7= 14

14 x 2 + 7 = 35

35 x 2 + 7 = 77

77 x 2 + 7 =  161

Correct option: A

Question 3. Find the missing number from the below series?

9, 81, —, 6561, 59049

Options:

A.  648

B.  729

C.  3281

D.  None of the above

Solution:     9

9 x 9 = 81

81 x 9 = 729

729 x 9 = 6561

6561 x 9 = 59049

Correct option: B

Type 5. How to Solve Number Series Questions Quickly  : Mixed series

  • Here the series is formulated by using more than one arithmetic logic.

Question 1.  Find out the missing numbers from the below series?

81, 80, 84, –, 91, 66, —, 53

Options:

A.)  88, 76

B.)  75, 102

C.)  76, 95

D.)  None of the above

Solution:    81+ 02= 81

81- 12= 80

80+ 22= 84

84- 32= 75

75+ 42= 91

91- 52= 66

66+ 62= 102

102- 72= 53

Correct option: B

Question 2.  There is one wrong number in the below series which is not following the series pattern. Find out that number?

39, 120, 365, 1092

Options:

A.  39

B.  365

C.  120

D.  1092

Solution:     12

12 x 3 + 3 = 39

39 x 3 + 3 = 120

120 x 3 + 3 = 363

Correct option: B

Question 3. Below series contains a wrong number, find the one which does not follow the series trend?

12, 61, 307, 7656, 38281

Options:

A.  12

B.  307

C.  61

D.  7656

E.  38281

Solution:    12 + 12 x 5+1= 61

61 x 5 +1= 306

306 x 5+1= 1531

1531 x 5+1= 7656

7656 x 5+1= 38281

Correct Option: B

Also Check Out

Questions to solve for Number Series
Formulas solve Number Series Questions quickly
Tips, Tricks and shortcuts for Number Series
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout